圆柱齿轮的有限元模态分析
摘要:为改善圆柱齿轮的动态特性,提高其工作的可靠性,以振动力学和有限元理论为基础,建立起了圆柱齿轮的有限元模型。计算出了其前6阶固有频率和固有振型,为圆柱齿轮的设计提供直接的理论依据,同时也为其动力响应的计算奠定了基础。
1 前言
圆柱齿轮是应用最广的传动零件之一,它传动效率高,传动比稳定,工作可靠性较高。但是若圆柱齿轮结构的非标设计不合理,其动态性能存在问题,在工作过程中会产生较大的振动和噪声,并会影响其工作精度和可靠性。对圆柱齿轮进行有限元模态分析,确定其固有频率和固有振型,避免系统工作时发生共振和出现有害振型,而且还可以找出齿轮的薄弱环节,为以后进一步进行齿轮的动力修改、噪声控制和优化设计奠定基础。圆柱齿轮的固有特性对其动力响应也有很大影响,动力响应是固有特性与激振力作用的综合表现。
2 建立圆柱齿轮有限元模型
(1)建立圆柱齿轮几何模型
为便于说明问题,取一个简化的圆柱齿轮模型进行模态分析:渐开线齿廓曲面简化为倾斜平面,忽略较小尺寸的圆角和倒角,个别尺寸予以修正。该齿轮的内径为2.2,齿根圆直径为3.8,齿顶圆直径为4.4,齿轮的齿根部分是齿根圆周长的2 3长,齿端部分是齿顶圆周长的2 7,齿轮齿数为24。计算
表明:这种简化对齿轮的动力学特性影响很小。
(2)有限元网格划分
圆柱齿轮为三维实体模型,在对圆柱齿轮几何模型划分有限元网格时,采用的单元为八节点六面体块单元,模型最终划分为3 072个单元,共有5 328个节点。
(3)边界条件处理
根据圆柱齿轮的的工作条件,齿轮和传动轴之间是过盈配合,齿轮内圆上各节点沿3个坐标轴方向的平动位移被约束。
(4)输入材料参数
齿轮的材料为各向同性材料,输入的材料性能参数有:材料的弹性模量E=2.06e11 Pa,泊松比μ=0.3,密度为7 800 kg m3。
3 模态计算和结果分析
(1)运动微分方程的建立
根据振动力学和有限元理论,圆柱齿轮的运动微分方程为

若无外力的作用,{f(t)}=0,得到系统的自由振动方程。在求解自由振动的固有频率和振型时,阻尼的影响不大,因此,阻尼可以忽略,这时,无阻尼自由振动的运动方程为

(2)圆柱齿轮的有限元模态分析结果
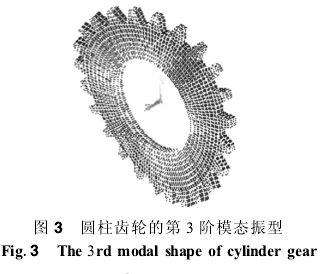
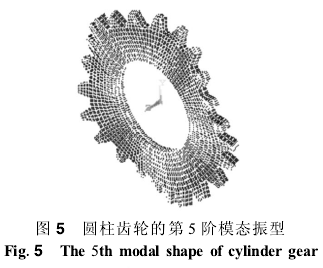
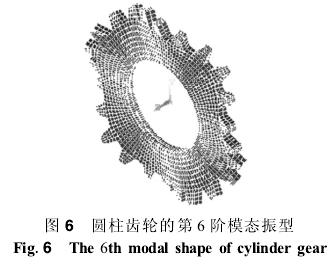
结构的振动可以表达为各阶固有振型的线性组合,其中低阶振型对结构的振动影响较大,对结构的动态特性起决定作用。对结构进行模态分析一般取前5~10阶即可。由于篇幅限制,这里计算出了圆柱齿轮的前六阶固有频率和振型。
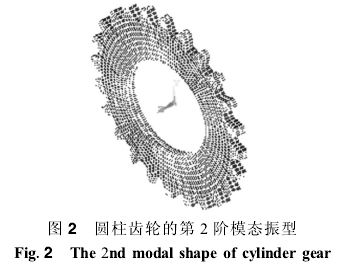
在有限元程序中调入上述有限元模型,经计算得到圆柱齿轮前六阶固有频率、振型见表1。振型图见图1~图6。需要指出的是,由于圆柱齿轮结构关于z轴中心对称,故对于振型对称的第2、第3、第4、第5、第6阶模态,其相应的频率均有重根。计算表明,结构的模态分布主要为扭转振动和弯曲振动,而且,齿根圆附近相对应力比较大,是结构的薄弱环节。
4 结语
(1)利用振型图,可直观地分析圆柱齿轮的动态特性并发现薄弱环节,为齿轮的动态性能实验、设计和维护提供理论依据,同时,也为结构系统的动态响应计算和分析打下基础。
(2)本研究方法可以很好地处理圆柱齿轮有限元模型的简化和建立等复杂情况,是一种较为精确和实用的计算分析方法。









