蜗轮蜗杆试验台疲劳测试及控制系统仿真
摘要:为了研究蜗轮蜗杆装置的疲劳特性,设计了一套蜗轮蜗杆疲劳测试试验台,通过一系列试验能准确测量出蜗轮蜗杆的疲劳寿
命;在此基础上建立该控制系统数学模型,并对控制系统进行MATLAB仿真;实验表明,其精度满足要求,并且系统工作稳定可靠。
疲劳试验机[1-2]是一种用于研究与检测材料、零部件、各类产品的力学性能与可靠性的测试仪器。它可广泛用于科学研究、能源交通、机械电子等各领域,是科研、生产部门必备的基本设备。试验机在材料试验、新型材料开发、产品设计、产品质量监督以及质量控制等方面都发挥着重要的作用。试验机可分为如下几类:金属材料试验机、非金属材料试验机、平衡机、无损检测仪器、振动台与冲击台、力与变形检测仪器、摩擦磨损、润滑与工艺试验机、包装件试验机、大型结构试验机及汽车专用测试设备等。疲劳试验机属于技术密集型的测试装置,目前它已经涉及到机械、液压、电子、材料、测量、自动控制等许多技术领域,并且还综合了近代闭环伺服、数字显示、机电一体化以及电子计算机等高新技术,被广泛应用于新材料开发,结构设计和机械、船舶、航空、航天、人体力学性能研究等方面。
1 蜗轮蜗杆疲劳试验台构成及控制原理
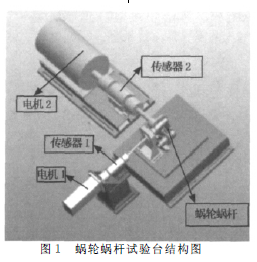
1.1 蜗轮蜗杆控制系统组成
蜗轮蜗杆试验台结构原理图如图1所示。本试验台包括三部分:第一部分是与蜗杆连接的永磁同步电机1和传感器1,其中电机1是速度控制模式,通过设定电机1的转速来控制蜗轮蜗杆转速,传感器1是扭矩传感器,用来测定蜗杆端的扭矩,其量程为±10Nm。第二部分是与蜗轮相连接的异步电机2和传感器2,其中电机2是扭矩控制模式,它作为负载,可以提供200Nm以下的任意扭矩,传感器2为扭矩传感器,其量程为±200Nm;第三部分是支架,它是起到支撑固定马达、传感器和蜗轮蜗杆装置的作用。
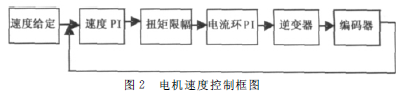
1.2 伺服电机速度和转矩控制
电机速度控制框图如图2所示,首先设定电机的运行速度,进入速度环中再经过系统滤波和PI控制器,经过PI计算后流入扭矩限幅模块。用户可以根据自己需要设定最大的电机扭矩值。当电机运行时,只要超过这个扭矩值,系统自动输出最大限制扭矩值,再经过PWM 逆变变成三相电压驱动电机。最后由编码器检测电机速度和位置值反馈进入速度设定,这是一个比较常见的闭环控制,保证了电机运行的高精度和稳定性。
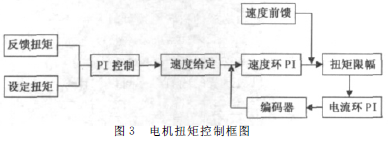
电机扭矩控制[3-5]框图如图3所示,首先在程序中标定扭矩值单位为Nm,再给定扭矩值作为扭矩环的输入。此时电机运行,扭矩传感器测量到实际的扭矩值,测量值和设定扭矩值进入PI控制器计算后给定到电机的速度环。进入速度环中再经过系统滤波和PI控制器,经过PI计算后流入扭矩限幅模块,用户可以根据自己需要设定最大的电机扭矩值,当电机运行时,只要超过这个扭矩值,系统自动只输出最大限制扭矩值,再经过PWM 逆变变成三相电压驱动电机,最后由编码器检测电机速度和位置值反馈进入速度环,同时在扭矩环中还加入了小电机的速度作为扭矩环的前馈补偿,这样既保证了电机速度的稳定也可以保证扭矩值的稳定。
通过系统中的这两种控制方法,首先保证了位置电机的速度和位置稳定,同时也保证了扭矩电机的扭矩值的稳定性。
2 蜗轮蜗杆疲劳试验台疲劳设定及目标曲线输入
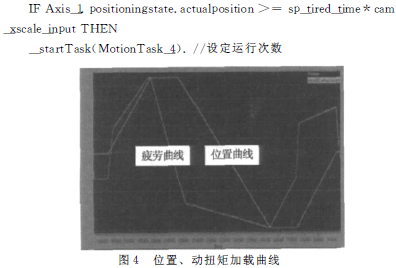
本蜗轮蜗杆试验台测试[6]的疲劳是通过上位机设定疲劳次数,来检测蜗轮蜗杆是否合格,而下位机通过设定疲劳曲线给定到伺服控制器中,速度电机运行位置曲线,扭矩电机运行扭矩曲线,两电机配合运行。加载目标曲线如图4所示。疲劳次数设定:虚拟轴启动,位置轴执行同步功能,通过计算虚拟轴的位置,因为虚拟轴是以匀速而且同方向运行,所以设定目标曲线X 轴长度的N 倍,也就是电机运行周期数,如果N 次次数达到了就停机去使能,没达到将会继续运行,中途如果出现报警就及时复位,程序如下:
3 蜗轮蜗杆试验台建模及仿真
蜗轮蜗杆试验台矢量简化图如图5所示。图中电机1的输出扭矩、转角、转动惯量和扭转刚度分别为Tm2 、θm2 、J2 、K2;电机2的输出扭矩、转角、转动惯量和扭转刚度分别为Tm1 、θm1 、J1 、K1 ;联轴器和传感器的转动惯量分别为J3 、J4 、J5 、J6 、J7 、J8 ;蜗轮蜗杆扭转刚度、质量、阻尼系数、摩擦系数、螺距分别为K0、m、c、u、L。把系统的力向同步电机1轴转化,可得到系统的力学方程式:

分传递函数,伺服系统电机输出转角F(S),输出Y(S)是蜗轮蜗杆转动位移。

结合蜗轮蜗杆电气伺服系统传递函数,它们共同组成了蜗轮蜗杆试验台MATLAB 仿真模型的传递函数框图如图6所示。
各部分传递函数及参数计算:
1)PWM (Pulse Width Modulation脉宽调制)逆变器,通过对一系列脉冲的宽度进行调制,来等效的获得所需要的波形(形状和幅值),PWM 逆变器可以简化成一阶惯性环节,传递函数为:
![]()
其中:KPWM为其时间常数,TPWM为PWM 逆变器的放大系数。
参考西门子电机使用手册可知:
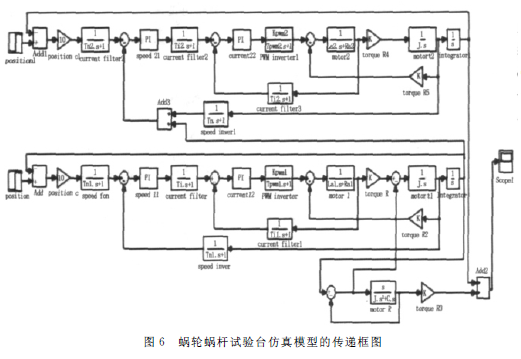
![]()
电枢绕组电阻Ra1 =0.12Ω,电枢绕组电感La1 =0.0016H;电枢绕组电阻Ra2 =0.2 Ω,电枢绕组电感La2 =0.0022H。
2)电流反馈滤波,由于脉宽调制的输出给反馈信号带来高次谐波分量,系统振荡系数增加,故需要增加滤波器,传递 函数一般可以表示为:
![]()
Ti为电流反馈滤波时间常数。
参考西门子电机手册可知:电流环反馈滤波时间常数Ti=100μs,速度环滤波时间常数Tn =0.01s,电流检测放大系数KP1 =1,速度检测放大系数KP2 =1。
3)机械系统参数计算:
转动惯量J02计算,转动惯量
J2 =9.0×10-4kg·m2J1=1.1×10-3kg·m2
由于传感器固定在台面上,故J8 =0.8×10-6kg·m2,联轴器3、4质量为0.2kg,直径为6cm,蜗杆质量为0.2kg,螺距L=1cm,传动轴总直径为1.5cm,质量为0.3kg,所以系统蜗杆端总转动惯量,对于空心圆柱体转动惯量(齿轮、联轴器、丝杠、轴)公式:
![]()
式中:M 为圆柱体质量,D1为圆柱体外径,D2为圆柱体内径。
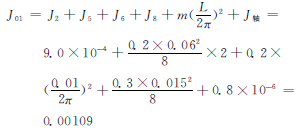
电机2端转动惯量计算,同理,由于传感器固定在台面上,故J7 =0.0004kg·m2,联轴器1、2质量为1kg、2kg,直径分别为12cm、15cm,蜗轮质量为1kg,直径为17cm,传动轴直径为6cm,质量为0.8kg,所以系统蜗杆端总转动惯量:

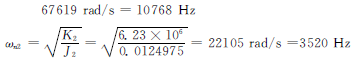
等效转动阻尼系数c,关于阻尼问题,目前有多种不同的阻尼理论,和相应的表达式,但对于本装置还是选择滞后阻尼理论来表示,在此参考相关的资料,取系统的相对阻尼比为ξ=0.01,由此反求等效阻尼。
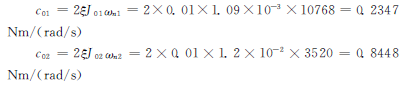
4)电流控制器参数计算:
电流检测放大系数Kp11 =0.001,速度环滤波时间常数Tn =0.01s,速度检测放大系数Kp12 =0.001。
系统积分时间常数:由于电机电气时间常数比SPWM 时间常数,为了降低惯性环节对系统的影响,提高电流环的响应速度,取调节器时间常数等于电机电气时间常数,即取:τI=Ts,得τI=Ts=0.0020s,那么:
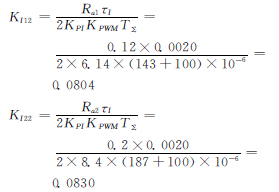
5)速度控制器参数计算:
在速度控制器中,考虑综合动态跟随性能,参考典型系统中频宽度参数表,取中频宽度h=4.3,那么速度环增益:
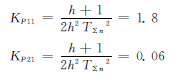
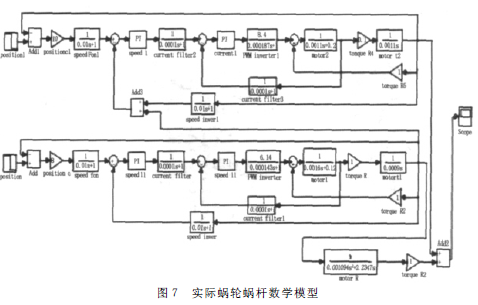
综上所述:把上述计算数据代入图6对应的参数中,就可以得到实际的蜗轮蜗杆数学模型如图7所示。
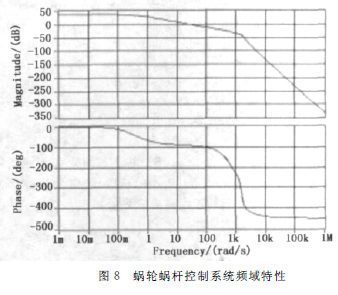
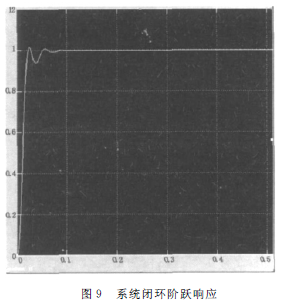
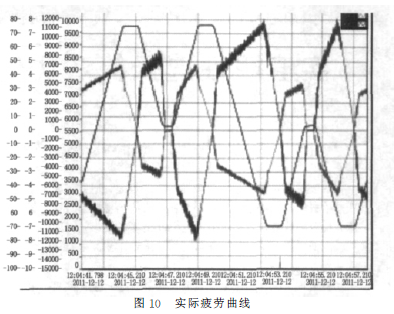
取仿真时间为1s,可得到控制系统闭环时域特性和频域特性,如图8、图9所示,系统采集的实际疲劳曲线如图10所示。
4 结论
分析频域[9]如图8所示,系统幅值裕度为Kg=30dB,相位裕度为r=85°,根据控制系统设计的准则,为了得到良好的控制性能,相位裕度应大于45°,系统就具有足够的幅值稳定裕度,而幅值裕度应大于6dB。所以从频域上分析系统稳定,而且满足相应的相位裕度和幅值裕度要求。分析系统闭环阶跃响应如图9所示,可以看出系统在启动到稳定状态无明显的振荡,故系统是稳定的。再分析系统采集的实际疲劳曲线如图10,与目标曲线图4相比较,曲线一致,系统精度维持在允许的范围。









